ACP-83: Dynamic Multidimensional Fees
Details for Avalanche Community Proposal 83: Dynamic Multidimensional Fees
| ACP | 83 |
|---|---|
| Title | Dynamic multidimensional fees for P-chain and X-chain |
| Author(s) | Alberto Benegiamo (@abi87) |
| Status | Stale |
| Track | Standards |
| Superseded-By | ACP-103 |
Abstract
Introduce a dynamic and multidimensional fees scheme for the P-chain and X-chain.
Dynamic fees helps to preserve the stability of the chain as it provides a feedback mechanism that increases the cost of resources when the network operates above its target utilization.
Multidimensional fees ensures that high demand for orthogonal resources does not drive up the price of underutilized resources. For example, networks provide and consume orthogonal resources including, but not limited to, bandwidth, chain state, read/write throughput, and CPU. By independently metering each resource, they can be granularly priced and stay closer to optimal resource utilization.
Motivation
The P-Chain and X-Chain currently have fixed fees and in some cases those fees are fixed to zero.
This makes transaction issuance predictable, but does not provide feedback mechanism to preserve chain stability under high load. In contrast, the C-Chain, which has the highest and most regular load among the chains on the Primary Network, already supports dynamic fees. This ACP proposes to introduce a similar dynamic fee mechanism for the P-Chain and X-Chain to further improve the Primary Network's stability and resilience under load.
However, unlike the C-Chain, we propose a multidimensional fee scheme with an exponential update rule for each fee dimension. The HyperSDK already utilizes a multidimensional fee scheme with optional priority fees and its efficiency is backed by academic research.
Finally, we split the fee into two parts: a base fee and a priority fee. The base fee is calculated by the network each block to accurately price each resource at a given point in time. Whatever amount greater than the base fee is burnt is treated as the priority fee to prioritize faster transaction inclusion.
Specification
We introduce the multidimensional scheme first and then how to apply the dynamic fee update rule for each fee dimension. Finally we list the new block verification rules, valid once the new fee scheme activates.
Multidimensional scheme components
We define four fee dimensions, Bandwidth, Reads, Writes, Compute, to describe transactions complexity. In more details:
Bandwidthmeasures the transaction size in bytes, as encoded by the AvalancheGo codec. Byte length is a proxy for the network resources needed to disseminate the transaction.Readsmeasures the number of DB reads needed to verify the transactions. DB reads include UTXOs reads and any other state quantity relevant for the specific transaction.Writesmeasures the number of DB writes following the transaction verification. DB writes include UTXOs generated as outputs of the transactions and any other state quantity relevant for the specific transaction.Computemeasures the number of signatures to be verified, including UTXOs ones and those related to authorization of specific operations.
For each fee dimension , we define:
- fee rate as the price, denominated in AVAX, to be paid for a transaction with complexity along the fee dimension .
- base fee as the minimal fee needed to accept a transaction. Base fee is given be the formula
- priority fee as an optional fee paid on top of the base fee to speed up the transaction inclusion in a block.
Dynamic scheme components
Fee rates are updated in time, to allow a fee increase when network is getting congested. Each new block is a potential source of congestion, as its transactions carry complexity that each validator must process to verify and eventually accept the block. The more complexity carries a block, and the more rapidly blocks are produced, the higher the congestion.
We seek a scheme that rapidly increases the fees when blocks complexity goes above a defined threshold and that equally rapidly decreases the fees once complexity goes down (because blocks carry less/simpler transactions, or because they are produced more slowly). We define the desired threshold as a target complexity rate : we would want to process every second a block whose complexity is . Any complexity more than that causes some congestion that we want to penalize via fees.
In order to update fees rates we track, per each block and each fee dimension, a parameter called cumulative excess complexity. Fee rates applied to a block will be defined in terms of cumulative excess complexity as we show in the following.
Suppose that a block is the current chain tip. has the following features:
- is its timestamp.
- is the cumulative excess complexity along fee dimension .
Say a new block is built on top of , with the following features:
- is its timestamp
- is its complexity along fee dimension .
Then the fee rate applied for the block along dimension will be:
where
- is the minimal fee rate along fee dimension
- is the target complexity rate along fee dimension
- is a normalization constant for the fee dimension
Moreover, once the block is accepted, the cumulative excess complexity is updated as follows:
The fee rate update formula guarantees that fee rates increase if incoming blocks are complex (large ) and if blocks are emitted rapidly (small ). Symmetrically, fee rates decrease to the minimum if incoming blocks are less complex and if blocks are produced less frequently.
The update formula has a few paramenters to be tuned, independently, for each fee dimension. We defer discussion about tuning to the implementation section.
Block verification rules
Upon activation of the dynamic multidimensional fees scheme we modify block processing as follows:
- Bound block complexity. For each fee dimension , we define a maximal block complexity . A block is only valid if the block complexity is less than the maximum block complexity: .
- Verify transaction fee. When verifying each transaction in a block, we confirm that it can cover its own base fee. Note that both base fee and optional priority fees are burned.
User Experience
How will the wallets estimate the fees?
AvalancheGo nodes will provide new APIs exposing the current and expected fee rates, as they are likely to change block by block. Wallets can then use the fees rates to select UTXOs to pay the transaction fees. Moreover, the AvalancheGo implementation proposed above offers a fees.Calculator struct that can be reused by wallets and downstream projects to evaluate calculate fees.
How will wallets be able to re-issue Txs at a higher fee?
Wallets should be able to simply re-issue the transaction since current AvalancheGo implementation drops mempool transactions whose fee rate is lower than current one. More specifically, a transaction may be valid the moment it enters the mempool and it won’t be re-verified as long as it stays in there. However, as soon as the transaction is selected to be included in the next block, it is re-verified against the latest preferred tip. If fees are not enough by this time, the transaction is dropped and the wallet can simply re-issue it at a higher fee, or wait for the fee rate to go down. Note that priority fees offer some buffer space against an increase in the fee rate. A transaction paying just the base fee will be evicted from the mempool in the face of a fee rate increase, while a transaction paying some extra priority fee may have enough buffer room to stay valid after some amount of fee increase.
How does priority fees guarantee a faster block inclusion?
AvalancheGo mempool will be restructured to order transactions by priority fees. Transactions paying priority fees will be selected for block inclusion first, without violating any spend dependency.
Backwards Compatibility
Modifying the fee scheme for P-Chain and X-Chain requires a mandatory upgrade for activation. Moreover, wallets must be modified to properly handle the new fee scheme once activated.
Reference Implementation
The implementation is split across multiple PRs:
- P-Chain work is tracked in this issue: https://github.com/ava-labs/avalanchego/issues/2707
- X-Chain work is tracked in this issue: https://github.com/ava-labs/avalanchego/issues/2708
A very important implementation step is tuning the update formula parameters for each chain and each fee dimension. We show here the principles we followed for tuning and a simulation based on historical data.
Tuning the update formula
The basic idea is to measure the complexity of blocks already accepted and derive the parameters from it. You can find the historical data in this repo.
To simplify the exposition I am purposefully ignoring chain specifics (like P-chain proposal blocks). We can account for chain specifics while processing the historical data. Here are the principles:
- Target block complexity rate : calculate the distribution of block complexity and pick a high enough quantile.
- Max block complexity : this is probably the trickiest parameter to set.
Historically we had pretty big transactions (more than referenced utxos). Setting a max block complexity so high that these big transactions are allowed is akin to setting no complexity cap.
On the other side, we still want to allow, even encourage, UTXO consolidation, so we may want to allow transactions like this.
A principled way to set max block complexity may be the following:
- calculate the target block complexity rate (see previous point)
- calculate the median time elapsed among consecutive blocks
- The product of these two quantities should gives us something like a target block complexity.
- Set the max block complexity to say the target value.
- Normalization coefficient : I suggest we size it as follows:
- Find the largest historical peak, i.e. the sequence of consecutive blocks which contained the most complexity in the shortest period of time
- Tune so that it would cause a increase in the fee rate for such a peak. This increase would push fees from the milliAVAX we normally pay under stable network condition up to tens of AVAX.
- Minimal fee rates : we could size them so that transactions fees do not change very much with respect to the currently fixed values.
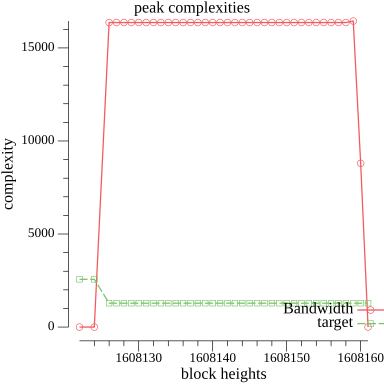
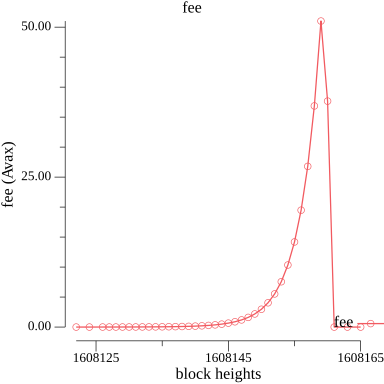
We simulate below how the update formula would behave on an peak period from Avalanche mainnet.
 />
/>
 />
/>
Figure 1 shows a peak period, starting with block wqKJcvEv86TBpmJY2pAY7X65hzqJr3VnHriGh4oiAktWx5qT1 and going for roughly 30 blocks. We only show Bandwidth for clarity, but other fees dimensions have similar behaviour.
The network load is much larger than target and sustained.
Figure 2 show the fee dynamic in response to the peak: fees scale up from a few milliAVAX up to around 25 AVAX. Moreover as soon as the peak is over, and complexity goes back to the target value, fees are reduced very rapidly.
Security Considerations
The new fee scheme is expected to help network stability as it offers economic incentives to users to hold transactions issuance in times of high load. While fees are expected to remain generally low when the system is not loaded, a sudden load increase, with fuller blocks, would push the dynamic fees algo to increase fee rates. The increase is expected to continue until the load is reduced. Load reduction happens by both dropping unconfirmed transactions whose fee-rate is not sufficient anymore and by pushing users that optimize their transactions costs to delay transaction issuance until the fee rate goes down to an acceptable level.
Note finally that the exponential fee update mechanism detailed above is proven to be robust against strategic behaviors of users delaying transactions issuance and then suddenly push a bulk of transactions once the fee rate is low enough.
Acknowledgements
Thanks to @StephenButtolph @patrick-ogrady and @dhrubabasu for their feedback on these ideas.
Copyright
Copyright and related rights waived via CC0.
Is this guide helpful?